Рассмотрим ламинарное движение идеальной (то есть без внутреннего трения) несжимаемой жидкости в изогнутой трубке разного диаметра. Мы уже знаем, что из уравнения непрерывности жидкости S⋅v = const. Какие ещё можно сделать выводы?
Рассмотрим трубку разного сечения:
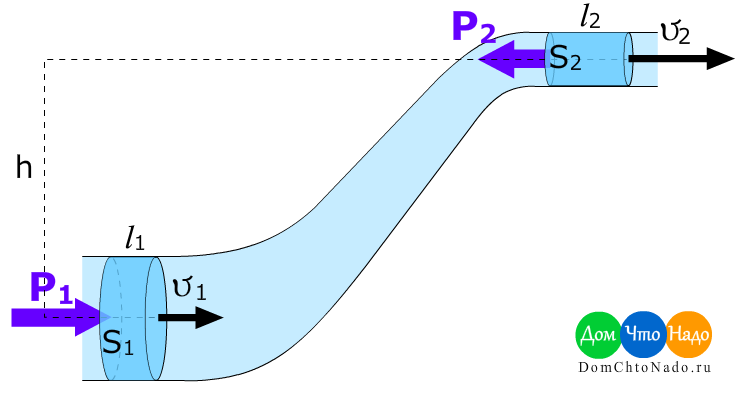
Возьмём срез жидкости в трубке. Из уравнения непрерывности следует, что при уменьшении сечения трубы увеличивается скорость потока жидкости. Если скорость увеличивается, значит по второму закону Ньютона действует сила F = m⋅a. Эта сила возникает за счет разности давления между стенками сечения потока жидкости. Значит сзади давление больше, чем спереди сечения. Это явление впервые описал Даниил Бернулли.
Закон Бернулли
В тех участках течения жидкости, где скорость больше давление меньше и наоборот.
Как любое тело, жидкость при перемещении совершает работу, т.е. выделяет энергию или поглощает. Закон сохранения энергии утверждает, что энергия тела никогда не исчезает и не появляется вновь, она может лишь превращаться из одного вида в другой. Этот закон универсален. В различных разделах физики он имеет свою формулировку.
Рассмотрим, какую работу совершает жидкость:
- Работа давления жидкости (EP). Давления жидкости выражается в том, что жидкость сзади давит на жидкость спереди.
- Работа по перемещению жидкости на высоту h (Eh). При опускании жидкости эта работа отрицательная, при поднятии - положительная.
- Работа по приданию скорости жидкости (Ev). При сужении трубки работа положительная, при расширении - отрицательная. Ещё это называют - кинетическая энергия или динамическое давление.
Так как мы рассматриваем идеальную жидкость, то трение отсутствует, а значит нет работы силы трения. Но в реальной жидкости она присутствует.
По закону сохранения энергии:
Ep + Eh + Ev = const
Давайте теперь определим, чем равняется каждая из этих работ.
Работа давления жидкости (EP)
Формула давления имеет вид: P = F/S, F = P⋅S. Работа силы создающая давление:
EP = P⋅S⋅ΔL = P⋅V
Работа по перемещению жидкости на высоту h (Eh)
Работа по перемещению жидкости на высоту h - это изменение потенциальной энергии которая равна:
Eh = m⋅g⋅h = V⋅ρ⋅g⋅h
Работа по приданию скорости жидкости (Ev)
Работа по приданию скорости жидкости - это кинетическая энергия, которая зависит от массы тела и его скорости и равна:
Ek = m⋅v2/2 = V⋅ρ⋅v2/2
Получим формулу сохранения энергии жидкости:
P⋅V + V⋅ρ⋅g⋅h + V⋅ρ⋅v2/2 = const
Сократим каждое слагаемое на V. Получим уравнение:
Формула Бернулли
P + ρ⋅g⋅h + ρ⋅v2/2 = const
Разделим каждый член последнего уравнения ρ⋅g, получим
| h + | P | + | v2 | = const | |
| ρ⋅g | 2g |
где h - геометрический напор, м;
P / ρ∙g - пьезометрический напор, м;
v2 / 2g - скоростной напор, м.
Полученное уравнение называется уравнением Бернулли для элементарной струйки идеальной жидкости. Оно было получено Даниилом Бернулли в 1738 году.
Сумма трех членов уравнения называется полным напором.
Или можно сказать по-другому - для идеальной движущейся жидкости сумма трех напоров: геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.
Уравнение Бернулли для потока реальной жидкости
Пусть поток реальной жидкости, обладающей вязкостью, движется в русле, ограниченном неподвижными стенками. При этом вследствие трения между слоями жидкости существенно возрастает неравномерность распределения скоростей по сечению потока.
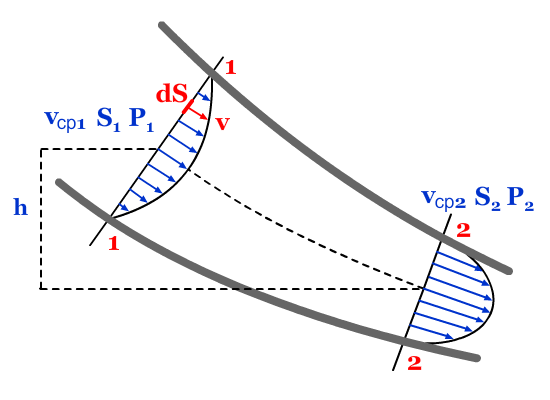
Также возникают потери энергии на трение при перемещении жидкости от одного сечения к другому. Кроме того, движение вязкой жидкости часто сопровождается вращением частиц, вихреобразованием и перемешиванием, что тоже требует затрат энергии.
Поэтому удельная энергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоления сопротивлений, и, следовательно, уменьшается вдоль потока.
Получим уравнение Бернулли для потока реальной жидкости, основываясь на том, что
оно является законом сохранения энергии для движущейся жидкости. Вывод этого уравнения проведем в два этапа. На первом этапе учтем неравномерность распределения скоростей по сечению потока, а на втором учтем и потери энергии.
При выводе будем считать, что в пределах выбранных сечений гидростатический
напор остается постоянным:
| h + | P | = const | |
| ρ⋅g |
const
g
p
z
.