Коэффициент теплопроводности

Мы уже знаем, что тепло передается от более теплого тела к менее теплому. Мы знаем, сколько нужно энергии, чтобы нагреть тело на определенное количество градусов. Но нам так же важно знать с какой скоростью проходит нагревание или остывание тела. Зная скорость остывания дома, мы можем определить с какой скоростью мы должны отапливать дом.

Скорость изменения температуры у всех тел разная. Все знают из личного опыта, что металл быстрее изменяет свою температуру, а вата медленнее, поэтому горячий поддон с пирожками из духовки мы достаем прихватками, а не руками. Рассмотрим теоретическую часть этого явления.

Опыт показывает, что передача тепла теплопроводностью происходит по нормали к изотермической поверхности от мест с большей температурой к местам с меньшей температурой.

Плотность теплового потока (q) - количество тепла, проходящее в единицу времени через единицу площади изотермической поверхности (вектор).

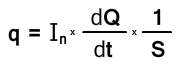
где dQ/dt - скорость теплового потока или количество тепла, проходящее в единицу времени, S - площадь изотермической поверхности, I_n - единичный вектор, направленный по нормали к изотермической поверхности в сторону уменьшения температуры.

В то же время Фурье вывел закон, что плотность теплового потока пропорциональна градиенту температуры и направлена в противоположную сторону:

q = -λ·grad(T) = -λ·dT/dn

Где λ − коэффициент теплопроводности и определяется для каждого тела экспериментальным путем, n - нормаль к изотермической поверхности.

Тепловой поток направлен от тепла к холоду, а температурный градиент в противоположную сторону, поэтому между ними знак минус.

Рассмотрим пример одномерной стационарной теплопроводности, возьмем стенку толщиной δ, которая намного меньше её ширины и длины.

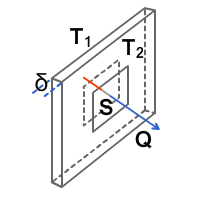
Условия стационарности:

∂t/∂x = ∂t/∂y = ∂t/∂z = 0;
dQ/dt = const = Q/t;
∇T = (T₂-T₁)/(x₂-x₁) = (T₂-T₁)/δ;

Используя определение плотности теплового потока и закон Фурье получим тождество:

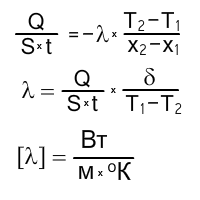
Где λ − коэффициент теплопроводности.

Физический смысл коэффициента теплопроводности - это количество тепла, протекающего в единицу времени через единицу площади изотермической поверхности при перепаде температуры в 1 Кельвин на единицу длины.

Для большинства материалов λ зависит от температуры тела и его зависимость определяется формулой:

λ = λ_о*(1-b(T-T_o))

Где λ_о - значение коэффициента теплопроводности при температуре T_o, b - постоянная, определяющаяся опытным путем.

Необходимо помнить следующее:

• Для кристаллов λ неодинаково в направлении различных осей кристалла. Для дерева λ различно вдоль и поперек волокон.
• Одни и тех же материалы с разной влажностью имеют разные λ.
• Коэффициент теплопроводности не является аддитивной величиной. Поэтому λ смеси не может быть рассчитано путем суммирования коэффициентов теплопроводности отдельных компонентов, из которых состоит смесь.
• Коэффициент теплопроводности сплава чистых металлов в общем случае не может быть средней величиной между коэффициентами теплопроводности чистых металлов, взятых в отдельности.
• При наличии разного рода примесей λ чистых металлов резко убывает.
• Для большинства газов, строительных и изоляционных материалов λ возрастает с возрастанием температуры.
• Строительные материалы с λ ≤ 0,23 Вт/(м⋅К) относят к теплоизоляционным материалам. Для большинства строительных и изоляционных материалов λ зависит от плотности, пористости, влажности и других факторов.
• Для большинства капельных жидкостей λ убывает с повышением температуры. Исключение составляют глицерин, вода и некоторые другие.
• Для одних металлов и сплавов (железо, углеродистая сталь и др.) λ убывает с увеличением температуры, для других (алюминий, нихром и др.) - увеличивается.
• Для большинства веществ зависимость коэффициента теплопроводности от температуры достаточно слабая, что позволяет его усреднять в заданном интервале температур и оперировать им как постоянной величиной.